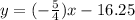Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (9,5)(9,5) and (-1,-3)(−1,−3).

Answer 1

`y=(-(5)/(4))x-16.25`

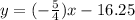
Explanation:

From the question we are told that:

Points of perpendicular bisector

(9,5),(−1,−3).

Generally the equation for slope is mathematically given by

`S=(y_2-y_1)/(x_2-x_1)`

`S=(-3-5)/(-1-9)`

`S=0.8`

`S=(4)/(5)`

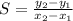
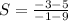
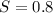
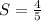
Therefore

Perpendicular lines of slope

`M=-(5)/(4)`

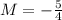
Generally the equation for perpendicular bisector Line is mathematically given by

`y-5=3(x-9)`

`y=(-(5)/(4))x-11.25+5`

`y=(-(5)/(4))x-16.25`