Given:
Principal = $14850
Rate of interest = 4% compounded semiannually.
Time = 3 years
To find:
The amount after 3 years.
Solution:
Formula for amount is:
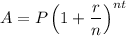
Where, P is principal, r is the rate of interest in decimal, n is the number of times interest compounded and t is the number of years.
The interest is compounded semiannually, so n=2.
Putting
 in the above formula, we get
in the above formula, we get
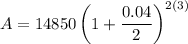
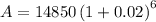
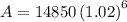
On further simplification, we get
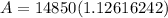

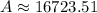
Therefore, the amount in the account after three years is $16723.51.