Question

If the sum of first n terms of an AP is 3n² + 5n find the AP.

Answer 1

Let a (n) denote the n-th term in the progression. Consecutive terms in the sequence differ by a fixed constant - call it c - such that

a (n) = a (n - 1) + c

Let a = a (1) be the first term in the sequence. We can solve for a (n) in terms of a alone:

a (n) = a (n - 1) + c

a (n) = (a (n - 2) + c) + c = a (n - 2) + 2c

a (n) = (a (n - 3) + c) + c = a (n - 3) + 3c

and so on, down to

a (n) = a + (n - 1) c

The sum of the first n terms is then

`\displaystyle\sum_(k=1)^n a(k)=\sum_(k=1)^n(a+(k-1)c)=a\sum_(k=1)^n1+c\sum_(k=1)^n(k-1)=an+\frac{cn(n-1)}2=\frac c2n^2+\left(a-\frac c2\right)n`

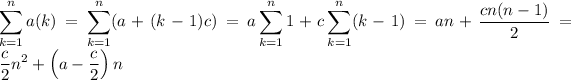
Since this is equal to 3n ^2 + 5n, it follows that

c/2 = 3 => c = 6

a - c/2 = 5 => a = 8

So the sequence is

a (n) = 8 + (n - 1) 6 = 6n + 2