Question

What is an equation of the line that passes through the points (6,-6) and (-2,-2)

Answer 1

`y=-(1)/(2)x-3`

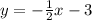
Explanation:

Hi there!

Linear equations are typically organized in slope-intercept form:
`y=mx+b` where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)

1) Determine the slope (m)

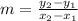`m=(y_2-y_1)/(x_2-x_1)` where the two given points are
`(x_1,y_1)` and
`(x_2,y_2)`

Plug in the given points (6,-6) and (-2,-2)

`=(-2-(-6))/(-2-6)\\=(-2+6)/(-2-6)\\=(4)/(-8)\\=-(1)/(2)`

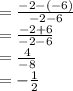
Therefore, the slope of the line is
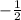`-(1)/(2)`. Plug this into
`y=mx+b`:

`y=-(1)/(2)x+b`

2) Determine the y-intercept (b)

`y=-(1)/(2)x+b`

Plug in one of the given points and solve for b

`-6=-(1)/(2)(6)+b\\-6=-3+b`

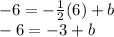
Add 3 to both sides

`-6+3=-3+b+3\\-3=b`

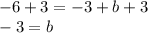
Therefore, the y-intercept of the line is -3. Plug this back into
`y=-(1)/(2)x+b`:

`y=-(1)/(2)x-3`

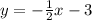
I hope this helps!