Answer:
see explanation
Explanation:
note that (sinx)² = sin²x
4sin²x - 2 = 0 ( add 2 to both sides )
4sin²x = 2 ( divide both sides by 4 )
sin²x =
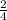 =
=
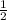 ( take square root of both sides )
( take square root of both sides )
sinx = ±
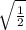 = ±
= ±
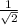
sinx =
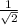 ( sinx > 0 , then x is in 1st/2nd quadrants )
( sinx > 0 , then x is in 1st/2nd quadrants )
x =
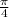 , π -
, π -
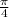 =
=
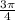
sinx = -
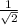 ( sinx < 0 , then x is in 3rd/4th quadrants )
( sinx < 0 , then x is in 3rd/4th quadrants )
x = π +
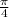 =
=
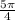 , 2π -
, 2π -
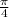 =
=
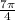
solutions are
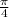 ,
,
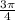 ,
,
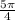 ,
,
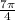 in the interval [ 0, 2π )
in the interval [ 0, 2π )