Differentiate the following by using "limit" \displaystyle (d)/(dx) √(x) ​​

Question

Differentiate the following by using "limit"


`\displaystyle (d)/(dx) √(x)`
​​

Answer 1

`\rm \displaystyle (d )/(dx) √(x) = ( 1 )/( 2√(x ) )`

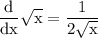
Explanation:

we want to differentiate the following by using limit:

`\displaystyle (d)/(dx) √(x)`

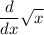
derivative definition by limit given by

`\rm \displaystyle (d)/(dx) = \lim _(\Delta x \to 0) \left( (f(x + \Delta x) - f(x))/( \Delta x) \right)`

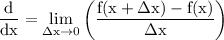
given that,

f(x)=√x

so,

f(x+∆x)=√(x+∆x)

thus substitute:

`\rm \displaystyle (d )/(dx) √(x) = \lim _(\Delta x \to 0) \left( ( √(x + \Delta x)- √(x) )/( \Delta x) \right)`

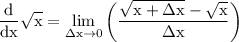
multiply both the numerator and denominator by the conjugate of the numerator:

`\rm \displaystyle (d )/(dx) √(x) = \lim _(\Delta x \to 0) \left( ( √(x + \Delta x)- √(x) )/( \Delta x) * ( √(x + \Delta x) + √(x) )/(√(x + \Delta x) + √(x)) \right)`

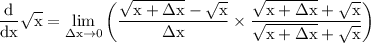
simplify which yields:

`\rm \displaystyle (d )/(dx) √(x) = \lim _(\Delta x \to 0) \left( ( (√(x + \Delta x)) ^(2) - x )/( \Delta x(√(x + \Delta x) + √(x))) \right)`

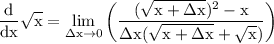
simplify square:

`\rm \displaystyle (d )/(dx) √(x) = \lim _( \Delta x \to 0) \left( ( x + \Delta x - x )/( \Delta x(√(x + \Delta x) + √(x))) \right)`

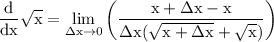
collect like terms:

`\rm \displaystyle (d )/(dx) √(x) = \lim _(\Delta x \to 0) \left( ( \Delta x )/( \Delta x(√(x + \Delta x) + √(x))) \right)`

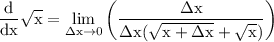
reduce fraction:

`\rm \displaystyle (d )/(dx) √(x) = \lim _(\Delta x \to 0) \left( ( 1 )/( (√(x + \Delta x) + √(x))) \right)`

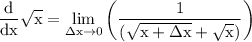
get rid of ∆x as we are approaching its to 0

`\rm \displaystyle (d )/(dx) √(x) = ( 1 )/( √(x ) + √(x))`

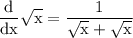
simplify addition:

`\rm \displaystyle (d )/(dx) √(x) = ( 1 )/( 2√(x ) )`

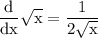
and we are done!