Given:
15.
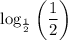
17.
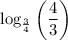
19.
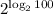
To find:
The values of the given logarithms by using the properties of logarithms.
Solution:
15. We have,
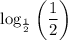
Using property of logarithms, we get

![[\because \log_aa=1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/rdi55arfjhwnzv5f81ix21xn87giv5lrtd.png)
Therefore, the value of
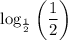 is 1.
is 1.
17. We have,
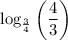
Using properties of logarithms, we get
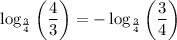
![[\because \log_a(m)/(n)=-\log_a(n)/(m)]](https://img.qammunity.org/2022/formulas/mathematics/college/7d89adbyl7g2ftvnor8yk71fc7wmj9cyqm.png)

![[\because \log_aa=1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/rdi55arfjhwnzv5f81ix21xn87giv5lrtd.png)
Therefore, the value of
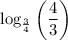 is -1.
is -1.
19. We have,
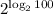
Using property of logarithms, we get
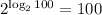
![[\because a^(\log_ax)=x]](https://img.qammunity.org/2022/formulas/mathematics/college/6smjnw045qxjv99ctrsminq68vhoohzzze.png)
Therefore, the value of
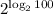 is 100.
is 100.