Given:
ABC is an isosceles triangle in which AC =BC.
D and E are points on BC and AC such that CE=CD.
To prove:
Triangle ACD and BCE are congruent.
Solution:
In triangle ACD and BCE,
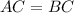 (Given)
(Given)

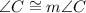 (Common angle)
(Common angle)
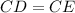 (Given)
(Given)
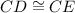
In triangles ACD and BCE two corresponding sides and one included angle are congruent. So, the triangles are congruent by SAS congruence postulate.
 (SAS congruence postulate)
(SAS congruence postulate)
Hence proved.