Question

ABC is an isosceles triangle in which AC =BC.

D and E are points on BC and AC such that CE=CD.
prove triangle ACD and BCE are congruent​

Answer 1

Given ABC is an isosceles triangle with AB=AC .D and E are the point on BC such that BE=CD

• Given AB=AC

∴∠ABD=∠ACE (opposite angle of sides of a triangle ) ....(1)

• Given BE=CD

Then BE−DE=CD−DE

ORBC=CE......................................(2)

In ΔABD and ΔACE

∠ABD=∠ACE ( From 1)

BC=CE (from 2)

AB=AC ( GIven)

∴ΔABD≅ΔACE

So AD=AE [henceproved]

Answer 2

Given:

ABC is an isosceles triangle in which AC =BC.

D and E are points on BC and AC such that CE=CD.

To prove:

Triangle ACD and BCE are congruent​.

Solution:

In triangle ACD and BCE,

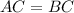`AC=BC` (Given)

`AC\cong BC`

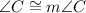`\angle C\cong m\angle C` (Common angle)

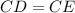`CD=CE` (Given)

`CD\cong CE`

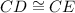
In triangles ACD and BCE two corresponding sides and one included angle are congruent. So, the triangles are congruent by SAS congruence postulate.

`\Delta ACD\cong \Delta BCE` (SAS congruence postulate)

Hence proved.