Question

If θ is an angle in standard position and its terminal side passes through the point (6,1), find the exact value of

sec
⁡
θ
secθ in simplest radical form.

Answer 1

Given:

θ is an angle in standard position.

Its terminal side passes through the point (6,1).

To find:

The exact value of secθ in simplest radical form.

Solution:

If θ is an angle in standard position and its terminal side passes through the point (x,y), then the exact value of secθ is:

`\sec\theta =(Hypotenuse)/(Base)`

`\sec\theta =(√(x^2+y^2))/(x)`

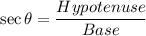
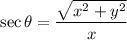
It is given that θ is an angle in standard position and its terminal side passes through the point (6,1), then the exact value of secθ is:

`\sec\theta =(√(6^2+1^2))/(6)`

`\sec\theta =(√(36+1))/(6)`

`\sec\theta =(√(37))/(6)`

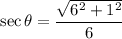
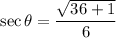
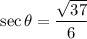
Therefore, the exact value of secθ is
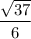`(√(37))/(6)`.