Given:
θ is an angle in standard position.
Its terminal side passes through the point (6,1).
To find:
The exact value of secθ in simplest radical form.
Solution:
If θ is an angle in standard position and its terminal side passes through the point (x,y), then the exact value of secθ is:
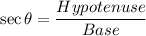
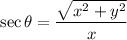
It is given that θ is an angle in standard position and its terminal side passes through the point (6,1), then the exact value of secθ is:
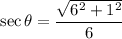
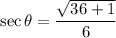
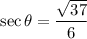
Therefore, the exact value of secθ is
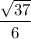 .
.