Answer:
Area of the shades region = 244.6 ft²
Explanation:
Area of the shaded region = Area of the rectangle ABCD- Area of the right angle triangle DEC
Area of the rectangle = Length × width
= 29.8 × 13
= 387.4 ft²
By applying Pythagoras theorem in the right triangle DEC,
(Hypotenuse)² = (leg 1)² + (leg 2)²
CD² = DE² + EC²
(29.8)² = DE² + (28)²
888.04 = DE² + 784
DE² = 888.04 - 784
DE = 10.2 ft
Area of ΔDEC =
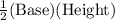
=
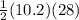
= 142.8 ft²
Area of the shades region = 387.4 - 142.8
= 244.6 ft²