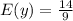Answer:
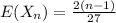
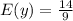
Explanation:
From the question we are told that:
Sample size n=9
Number of Green
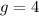
Number of yellow

Number of white
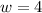
Probability of Green Followed by yellow P(GY) ball
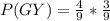
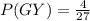
Generally the equations for when n is even is mathematically given by
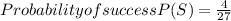
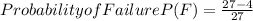
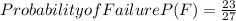
Therefore
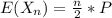
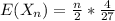
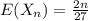
Generally the equations for when n is odd is mathematically given by
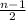
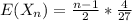
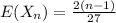
b)
Probability of drawing white ball
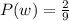
Therefore
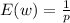
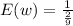
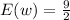
Therefore
/(9)](https://img.qammunity.org/2022/formulas/mathematics/high-school/4cq3dkj00ztkfx4w9vpq590xr96kkxj5bu.png)
/(9)](https://img.qammunity.org/2022/formulas/mathematics/high-school/thix9mz38n3g2wvpe1psz9r9hpn4jr6r79.png)