Given:
Consider the below figure attached with this question.
To find:
The measure of angle 3.
Solution:
According to intersecting secant theorem, if two secants of a circle intersect each other outside the circle, then the angle on the intersection is half of the difference of the intercepted arc.
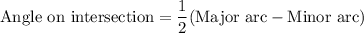
Using the intersecting secant theorem, we get
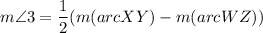
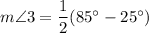
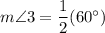

Therefore, the measure of angle 3 is 30 degrees.