The question is incomplete, the complete question is:
A certain substance X has a normal freezing point of
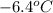 and a molal freezing point depression constant
and a molal freezing point depression constant
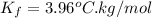 . A solution is prepared by dissolving some glycine in 950. g of X. This solution freezes at
. A solution is prepared by dissolving some glycine in 950. g of X. This solution freezes at
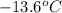 . Calculate the mass of urea that was dissolved. Round your answer to 2 significant digits.
. Calculate the mass of urea that was dissolved. Round your answer to 2 significant digits.
Answer: 129.66 g of glycine will be dissolved.
Step-by-step explanation:
Depression in the freezing point is the difference between the freezing point of the pure solvent and the freezing point of the solution.
The expression for the calculation of depression in freezing point is:
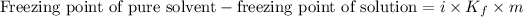
OR
![\text{Freezing point of pure solvent}-\text{freezing point of solution}=i* K_f* \frac{\text{Given mass of solute}* 1000}{\text{Molar mass of solute}* \text{Mass of solvent (g)}}]() ....(1)
....(1)
where,
i = Van't Hoff factor = 1 (for non-electrolytes)
Freezing point of pure solvent =
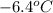
Freezing point of solution =
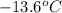
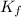 = freezing point depression constant =
= freezing point depression constant =
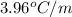
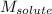 = Molar mass of solute (glycine) = 75.07 g/mol
= Molar mass of solute (glycine) = 75.07 g/mol
 = Mass of solvent = 950 g
= Mass of solvent = 950 g
Plugging values in equation 1:
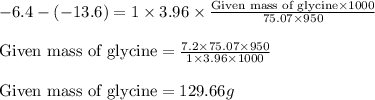
Hence, 129.66 g of glycine will be dissolved.