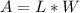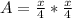Question

Mr. Jones' other friend Ms. O'Neill has "x" meters of fencing, what is the maximum area in square meters she can have?

Answer 1

`Max\ Area = (x^2)/(16)`

Explanation:

Given

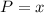`P = x` ---- the perimeter of fencing

Required

The maximum area

Let

`L \to Length`

`W \to Width`

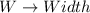
So, we have:

`P = 2(L + W)`

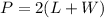
This gives:

`2(L + W) = x`

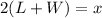
Divide by 2

`L + W = (x)/(2)`

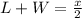
Make L the subject

`L = (x)/(2) - W`

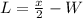
The area (A) of the fence is:

`A = L * W`

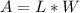
Substitute
`L = (x)/(2) - W`

`A = ((x)/(2) - W) * W`

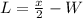
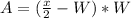
Open bracket

`A = (x)/(2)W - W^2`

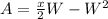
Differentiate with respect to W

`A' = (x)/(2) - 2W`

Set to 0

`(x)/(2) - 2W = 0`

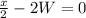
Solve for 2W

`2W = (x)/(2)`

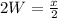
Solve for W

`W = (x)/(4)`

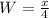
Recall that:

`L = (x)/(2) - W`

`L = (x)/(2) - (x)/(4)`

`L = (2x- x)/(4)`

`L = (x)/(4)`

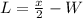
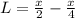
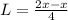
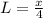
So, the maximum area is:

`A = L * W`

`A = (x)/(4)*(x)/(4)`

`Max\ Area = (x^2)/(16)`