Question

What is the exact time t, in years, needed for the balance of an account that earns 5% annual 8. Interest compounded continuously to triple?

Answer 1

It takes 22.52 years for the balance to triple in value.

Explanation:

Continuous compounding:

The amount of money earned using continuous compounding is given by the following equation:

`A(t) = A(0)(1+r)^t`

In which A(0) is the initial amount of money and r is the interest rate, as a decimal.

Interest rate of 5%.

This means that
`r = 0.05`, and thus:

`A(t) = A(0)(1+r)^t`

`A(t) = A(0)(1+0.05)^t`

`A(t) = A(0)(1.05)^t`

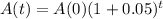
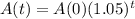
Time for the balance to triple?

This is t for which
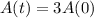`A(t) = 3A(0)`. So

`A(t) = A(0)(1.05)^t`

`3A(0) = A(0)(1.05)^t`

`(1.05)^t = 3`

`\log{(1.05)^t} = \log{3}`

`t\log{1.05} = \log{3}`

`t = \frac{\log{3}}{\log{1.05}}`

`t =  22.52`

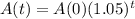
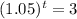
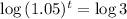
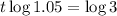
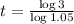
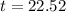
It takes 22.52 years for the balance to triple in value.