Answer:
It takes 22.52 years for the balance to triple in value.
Explanation:
Continuous compounding:
The amount of money earned using continuous compounding is given by the following equation:
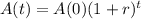
In which A(0) is the initial amount of money and r is the interest rate, as a decimal.
Interest rate of 5%.
This means that
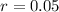 , and thus:
, and thus:
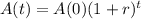
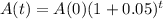
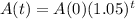
Time for the balance to triple?
This is t for which
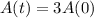 . So
. So
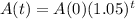
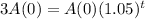
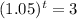
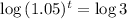
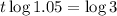
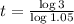
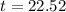
It takes 22.52 years for the balance to triple in value.