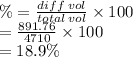18.9% is the answer
Explanation:
volume of a cylinder = πd²/4 x h
where d is diameter and h is height of cylinder.
thus
vol of A is
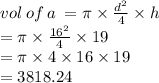
and
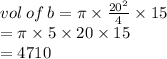
difference in vol of a and b is
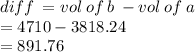
this volume will remain empty after container A is pumped into container B.
this volume as a percentage of total volume of B is