Answer:
The measure of the angle ACB is 59°.
Explanation:
Let be
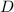 the location of the center of circle and
the location of the center of circle and
 is the radius of the figure, the triangles ACD and BCD are isosceles triangles, since
is the radius of the figure, the triangles ACD and BCD are isosceles triangles, since
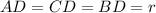 . And the measure of the angle C associated with each triangle are, respectively:
. And the measure of the angle C associated with each triangle are, respectively:
Triangle ACD
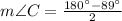
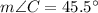
Triangle BCD
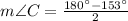

Lastly, the measure of the angle ACB is:
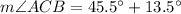
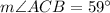
The measure of the angle ACB is 59°.