Question

In the diagram of a circle shown below, m AC = 89° and m BC = 153°. Determine m∠ACB.

Answer 1

The measure of the angle ACB is 59°.

Explanation:

Let be
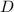`D` the location of the center of circle and
`r` is the radius of the figure, the triangles ACD and BCD are isosceles triangles, since
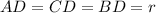`AD = CD = BD = r`. And the measure of the angle C associated with each triangle are, respectively:

Triangle ACD

`m\angle C = (180^(\circ)-89^(\circ))/(2)`

`m\angle C = 45.5^(\circ)`

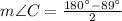
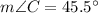
Triangle BCD

`m \angle C = (180^(\circ)-153^(\circ))/(2)`

`m\angle C = 13.5^(\circ)`

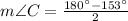
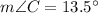
Lastly, the measure of the angle ACB is:

`m\angle ACB = 45.5^(\circ) + 13.5^(\circ)`

`m\angle ACB = 59^(\circ)`

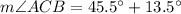
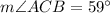
The measure of the angle ACB is 59°.