Answer:
a. 0.94 = 94% probability that the firm will make at least one hire.
b. The expected value of the number of hires is 1.7, and the standard deviation is 0.8062.
Explanation:
There is only a 6% chance that it will not make any hires
This means that P(X = 0) = 0.06.
16% chance that it will make all three hires.
This means that
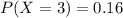
60% chance of hiring at least two candidates.
This means that:

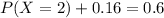

Probability of one hire:
The sum of all probabilities, from no hires to three hires, is 1. So
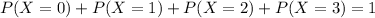
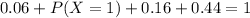
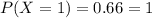
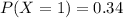
a. What is the probability that the firm will make at least one hire?
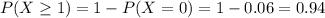
0.94 = 94% probability that the firm will make at least one hire.
b. Find the expected value and the standard deviation of the number of hires.
Expected value:
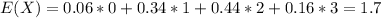
Standard deviation:

The expected value of the number of hires is 1.7, and the standard deviation is 0.8062.