Question

The liquid and gaseous state of hydrogen are in thermal equilibrium at 20.3 K. Even though it is on the point of condensation, model the gas as ideal and determine the most probable speed of the molecules (in m/s). What If? At what temperature (in K) would an atom of xenon in a canister of xenon gas have the same most probable speed as the hydrogen in thermal equilibrium at 20.3 K?

Answer 1

a) the most probable speed of the molecules is 409.2 m/s

b) required temperature of xenon is 1322 K

Step-by-step explanation:

Given the data in the question;

a)

Maximum probable speed of hydrogen molecule (H₂)

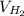`V_{H_2` = √( 2RT /
`M_{H_2` )

where R = 8.314 m³.Pa.K⁻¹.mol⁻¹ and given that T = 20.3 K

molar mass of H₂;
`M_{H_2` = 2.01588 g/mol

we substitute

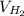`V_{H_2` = √( (2 × 8.314 × 20.3 ) / 2.01588 × 10⁻³ )

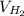`V_{H_2` = √( 337.5484 / 2.01588 × 10⁻³ )

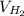`V_{H_2` = 409.2 m/s

Therefore, the most probable speed of the molecules is 409.2 m/s

b)

Temperature of xenon = ?

Temperature of hydrogen = 20.3 K

we know that;

T = (Vxe² × Mxe) / 2R

molar mass of xenon; Mxe = 131.292 g/mol

so we substitute

T = ( (409.2)² × 131.292 × 10⁻³) / 2( 8.314 )

T = 21984.14167 / 16.628

T = 1322 K

Therefore, required temperature of xenon is 1322 K