Question

To test this series for convergence

∝
∑ (4^n+7)/7^n
n=1
You could use the limit comparison test, comparing it to the series
∝
∑ r^n
n=1

Where r=???
Completing the test, it shows the series:

Answer 1

r should be 4/7. You're comparing the given series to a geometric series that converges. By the limit comparison test, you have

`\displaystyle\lim_(n\to\infty)((4^n+7)/(7^n))/((4^n)/(7^n))=\lim_(n\to\infty)(4^n+7)/(4^n)=\lim_(n\to\infty)\left(1+\frac7{4^n}\right)=1`

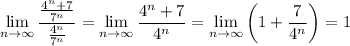
and since this limit is positive and finite, and the series you're comparing to is convergent, then the first series must also be convergent.