r should be 4/7. You're comparing the given series to a geometric series that converges. By the limit comparison test, you have
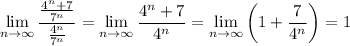
and since this limit is positive and finite, and the series you're comparing to is convergent, then the first series must also be convergent.