Question

You will purchase some cds and dvds. If you purchase 13 cds and 5 dvds, it will cost you $96.70; if you purchase 5 cds and 12 dvds, it will cost you $134.50. Write and solve a system of equations to solve.

Answer 1

Question

You will purchase some cds and dvds. If you purchase 13 cds and 5 dvds, it will cost you $96.70; if you purchase 5 cds and 12 dvds, it will cost you $134.50. Write and solve a system of equations to solve for the cost of each cd and the cost of each dvd.

Answer:

Cost of cd = $3.72

Cost of dvd = $9.66

Explanation:

Let the cost of a cd be c

Let the cost of a dvd be d

From the second statement:

If you purchase 13 cds and 5 dvds, it will cost you $96.70

This means that

13c + 5d = 96.70 ----------------(i)

Also, from the third statement:

if you purchase 5 cds and 12 dvds, it will cost you $134.50

This means that;

5c + 12d = 134.50 ---------------------(ii)

The equations to solve are equations (i) and (ii)

13c + 5d = 96.70

5c + 12d = 134.50

Multiply the first equation by 5 and the second equation by 13. i.e

5 x (13c + 5d = 96.70)

13 x (5c + 12d = 134.50)

This will give

65c + 25d = 483.5

65c + 156d = 1748.5

Find the difference of the two equations

65c + 25d = 483.5

-

65c + 156d = 1748.5

0 - 131d = - 1265

This gives;

-131d = -1265

Divide both sides by -131

`(-131d)/(-131) = (-1265)/(-131)`

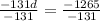
d = 9.66

This means that the cost of a dvd which is d = $9.66

Now substitute the value of d = 9.66 into equation (i) as follows;

13c + 5(9.66) = 96.70

Expand the above and solve for c

13c + 48.3 = 96.70

13c = 48.4

c =
`(48.4)/(13)`

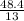
c = 3.72

This means that the cost of a cd which is c = $3.72