Question
You will purchase some cds and dvds. If you purchase 13 cds and 5 dvds, it will cost you $96.70; if you purchase 5 cds and 12 dvds, it will cost you $134.50. Write and solve a system of equations to solve for the cost of each cd and the cost of each dvd.
Answer:
Cost of cd = $3.72
Cost of dvd = $9.66
Explanation:
Let the cost of a cd be c
Let the cost of a dvd be d
From the second statement:
If you purchase 13 cds and 5 dvds, it will cost you $96.70
This means that
13c + 5d = 96.70 ----------------(i)
Also, from the third statement:
if you purchase 5 cds and 12 dvds, it will cost you $134.50
This means that;
5c + 12d = 134.50 ---------------------(ii)
The equations to solve are equations (i) and (ii)
13c + 5d = 96.70
5c + 12d = 134.50
Multiply the first equation by 5 and the second equation by 13. i.e
5 x (13c + 5d = 96.70)
13 x (5c + 12d = 134.50)
This will give
65c + 25d = 483.5
65c + 156d = 1748.5
Find the difference of the two equations
65c + 25d = 483.5
-
65c + 156d = 1748.5
0 - 131d = - 1265
This gives;
-131d = -1265
Divide both sides by -131
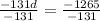
d = 9.66
This means that the cost of a dvd which is d = $9.66
Now substitute the value of d = 9.66 into equation (i) as follows;
13c + 5(9.66) = 96.70
Expand the above and solve for c
13c + 48.3 = 96.70
13c = 48.4
c =
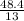
c = 3.72
This means that the cost of a cd which is c = $3.72