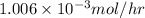Question

A) The average molecular speed in a sample of Ar gas at a certain temperature is 391 m/s. The average molecular speed in a sample of Ne gas is ______ m/s at the same temperature.

B) The rate of effusion of Xe gas through a porous barrier is observed to be 7.03×10-4 mol / h. Under the same conditions, the rate of effusion of SO2 gas would be ______ mol / h

Answer 1

For A: The average molecular speed of Ne gas is 553 m/s at the same temperature.

For B: The rate of effusion of
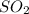`SO_2` gas is
`1.006* 10^(-3)mol/hr`

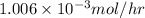
Step-by-step explanation:

For A:

The average molecular speed of the gas is calculated by using the formula:

`V_(gas)=\sqrt{(8RT)/(\pi M)}`

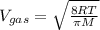
OR

`V_(gas)\propto \sqrt{(1)/(M)}`

where, M is the molar mass of gas

Forming an equation for the two gases:

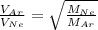`(V_(Ar))/(V_(Ne))=\sqrt{(M_(Ne))/(M_(Ar))}` .....(1)

Given values:

`V_(Ar)=391m/s\\M_(Ar)=40g/mol\\M_(Ne)=20g/mol`

Plugging values in equation 1:

`(391m/s)/(V_(Ne))=\sqrt{(20)/(40)}\\\\V_(Ne)=391* √(2)=553m/s`

Hence, the average molecular speed of Ne gas is 553 m/s at the same temperature.

For B:

Graham's law states that the rate of diffusion of a gas is inversely proportional to the square root of the molar mass of the gas. The equation for this follows:

`Rate\propto (1)/(√(M))`

Where, M is the molar mass of the gas

Forming an equation for the two gases:

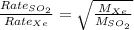`(Rate_(SO_2))/(Rate_(Xe))=\sqrt{(M_(Xe))/(M_(SO_2))}` .....(2)

Given values:

`Rate_(Xe)=7.03* 10^(-4)mol/hr\\M_(Xe)=131g/mol\\M_(SO_2)=64g/mol`

Plugging values in equation 2:

`(Rate_(SO_2))/(7.03* 10^(-4))=\sqrt{(131)/(64)}\\\\Rate_(SO_2)=7.03* 10^(-4)* \sqrt{(131)/(64)}\\\\Rate_(SO_2)=1.006* 10^(-3)mol/hr`

Hence, the rate of effusion of
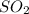`SO_2` gas is
`1.006* 10^(-3)mol/hr`