Answer: B. 4.11
Explanation:
Using Binomial distribution ( as the arrival times of workers are independent).
Formula for standard deviation:
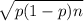 , where p= population proportion, n= sample size.
, where p= population proportion, n= sample size.
As per given ,
p= 0.06, n=300
Required standard deviation=

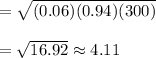
Hence, the correct option is B.