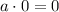Answer:
The equation
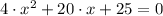 is equal to
is equal to
 .
.
Explanation:
Let be the equation
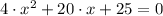 , we proceed to rewrite the equation solely by algebraic means:
, we proceed to rewrite the equation solely by algebraic means:
1)
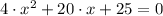 Given
Given
2)
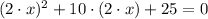 Definition of power/Associative property
Definition of power/Associative property
3)
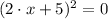 Perfect square trinomial
Perfect square trinomial
4)
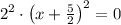 Distributive property/
Distributive property/
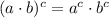
5)
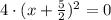 Definition of power
Definition of power
6)
 Compatibility with multiplication/Commutative and modulative properties/
Compatibility with multiplication/Commutative and modulative properties/