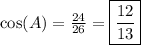Answer:
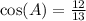
Explanation:
Without loss of generality, let
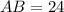 and
and
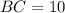 (follows tan(C)=2.4). In a right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side and the cosine of an angle is equal to its adjacent side divided by the hypotenuse.
(follows tan(C)=2.4). In a right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side and the cosine of an angle is equal to its adjacent side divided by the hypotenuse.
We can use the Pythagorean Theorem (
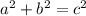 , where
, where
 is the hypotenuse) to solve for the hypotenuse:
is the hypotenuse) to solve for the hypotenuse:
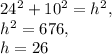
Therefore,