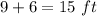Question

The area of a rectangular wall of a barn is 135 square feet. It's length is 6 feet longer than a width. Find the length and width of the wall of the barn

Answer 1

Answer:
`15\ ft,6\ ft`

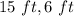
Explanation:

Given

The area of a rectangular wall of a barn is
`135\ ft^2`

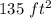
Suppose the width of the wall is
`x`

So, the length of the wall is
`6+x`

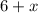
Area can be written as the product of length and width

`\Rightarrow (6+x)x=135\\\Rightarrow 6x+x^2=135\\\Rightarrow x^2+6x-135=0\\\Rightarrow x=(-6\pm √(6^2-4(1)(-135)))/(2(1))\\\\\Rightarrow x=(-6\pm 24)/(2)\\\\\Rightarrow x=-15,9`

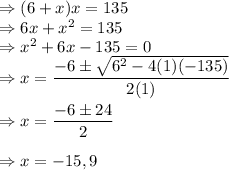
neglecting the negative value, width of the wall is
`9\ ft`

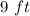
So, the length of the wall is
`9+6=15\ ft`