Answer:
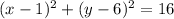
Explanation:
The equation of a circle is given by
 , where
, where
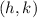 is the center of the circle and
is the center of the circle and
 is the radius of the circle.
is the radius of the circle.
From the diagram, we can find the following:
- the radius of the circle is 4
- the center of the circle is located at (1,6)
Thus, we have:
