Question

Please help me I’m lost

Answer 1

We are given with an equation and need to find it's solution set also we are given with a condition that m ≠ {0, 1} . So , let's start ;

So we are given with :

`{:\implies \quad \sf (6)/(m)+2=(m+3)/(m-1)}`

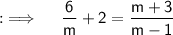
First , we will simplify the given Equation and then we will solve it . So , now taking LCM in LHS ;

`{:\implies \quad \sf (6+2m)/(m)=(m+3)/(m-1)}`

Now , Cross Multiplying ;

`{:\implies \quad \sf (m-1)(6+2m)=m(m+3)}`

`{:\implies \quad \sf m(6+2m)-1(6+2m)=m^(2)+3m}`

`{:\implies \quad \sf 6m+2m^(2)-6-2m=m^(2)+3m}`

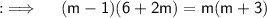
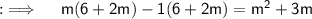
Now , transposing whole RHS to LHS and collecting like terms ;

`{:\implies \quad \sf (2m^(2)-m^(2))+(6m-2m-3m)-6=0}`

`{:\implies \quad \sf m^(2)+m-6=0}`

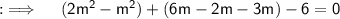
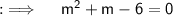
Now , we will solve this by splitting the Middle term ;

`{:\implies \quad \sf m^(2)+3m-2m-6=0}`

`{:\implies \quad \sf m(m+3)-2(m+3)=0}`

`{:\implies \quad \sf (m+3)(m-2)=0}`

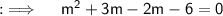
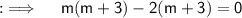
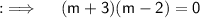
So , now either , m+3 = 0 or m-2 = 0 . On simplification we will get , m = 2 , -3. So m = {-3, 2}

Hence Option 1) {-3, 2} is correct