We are given with an equation and need to find it's solution set also we are given with a condition that m ≠ {0, 1} . So , let's start ;
So we are given with :
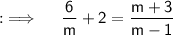
First , we will simplify the given Equation and then we will solve it . So , now taking LCM in LHS ;
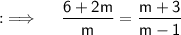
Now , Cross Multiplying ;
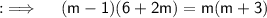
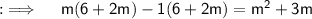
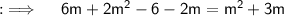
Now , transposing whole RHS to LHS and collecting like terms ;
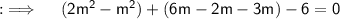
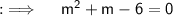
Now , we will solve this by splitting the Middle term ;
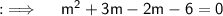
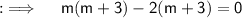
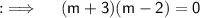
So , now either , m+3 = 0 or m-2 = 0 . On simplification we will get , m = 2 , -3. So m = {-3, 2}
Hence Option 1) {-3, 2} is correct