Answer:
Explanation:
Here we have been provided with the values of n and w that is 4 and -6 respectively.
Equation that we have,
Substituting the values of n and w in the equation,
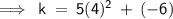
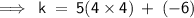
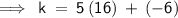
Multiplying 16 by 5,
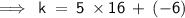
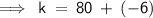
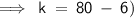
Subtracting 6 from 80,
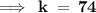
Therefore, value of k is 74..!!