Question

Find the unique permutations of the letters of the word : CEASELESS

Answer 1

There are 2,520 unique permutations.

Explanation:

When we have a set of N different elements, the total number of permutations is given by:

P = N! = N*(N - 1)*(N - 2)*...*(2)*(1)

Particularly, if out of these N elements, there are a given element that is repeated K times, then the permutations of these K elements actually do not add new unique permutations, then in that case the total number of unique permutations is:

P = N!/K!

And if we have another element that is repeated L times, then with the same reasoning than above, the total number of unique permutations is:

P = N!/(K!*L!)

Now, we have the set:

{C, E, A, S, E, L, E, S, S}

So we have a set of 9 letters, then:

N = 9

And, the letter S is repeated 3 times

The letter E is repeated 3 times

Then, using the above notation, we can define:

K = 3

L = 3

The total number of permutations is then:

`P = (9!)/(3!*3!) = (9*8*7*6*5*4*3*2*1)/(3*2*1*3*2*1) = (9*8*7*6*5*4)/(3*2*1) = 2,520`

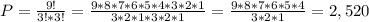
So there are 2,520 unique permutations.