Answer:
see below
Explanation:
we are given
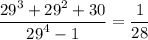
we want to prove it algebraically
to do so rewrite 30:
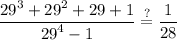
let 29 be a thus substitute:
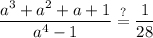
factor the denominator:
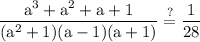
Factor out a²:
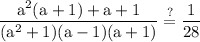
factor out 1:
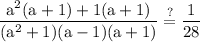
group:
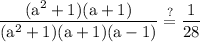
reduce fraction:
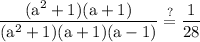
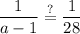
substitute back:
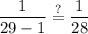
simplify substraction:
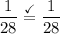
hence Proven