Question

For what value of c does x^2−2x−c=4 have exactly one real solution?
PLEASE HELP!!!!!!!

Answer 1

-5

Explanation:

Moving all terms of the quadratic to one side, we have

`x^2-2x-(c+4)=0`.

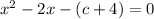A quadratic has one real solution when the discriminant is equal to 0. In a quadratic
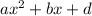`ax^2+bx+d`, the discriminant is
`√(b^2-4ad)`.

(The discriminant is more commonly known as
`√(b^2-4ac)`, but I changed the variable since we already have a
`c` in the quadratic given.)

In the quadratic above, we have
`a=1`,
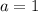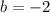`b=-2`, and
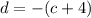`d=-(c+4)`. Plugging this into the formula for the discriminant, we have

`\sqrt{(-2)^2-4(1)(-(c+4))`.

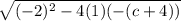Using the distributive property to expand and simplifying, the expression becomes

`√(4-4(-c-4))=√(4+4c+16)\\~~~~~~~~~~~~~~~~~~~~~~=√(20+4c)\\~~~~~~~~~~~~~~~~~~~~~~=√(4)\cdot√(5+c)\\~~~~~~~~~~~~~~~~~~~~~~=2√(c+5).`

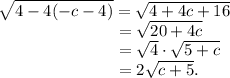
Setting the discriminant equal to 0 gives

`2√(c+5)=0`.

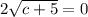We can then solve the equation as usual: first, divide by 2 on both sides:

`√(c+5)=0`.

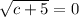Squaring both sides gives

`c+5=0`,

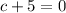and subtracting 5 from both sides, we have

`\boxed{c=-5}.`