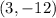Question

Put the quadratic into vertex form and state the coordinates of the vertex. y= y= \,\,x^2-6x-3 x 2 −6x−3

Answer 1

`y = (x - 3)^2 - 12`

`(3,-12)`

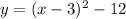
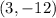
Explanation:

Given

`y = x^2 - 6x - 3`

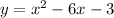
Solving (a): In vertex form

The vertex form of an equation is:

`y = a(x - h)^2 + k`

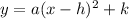
To do this, we make use of completing the square method.

We have:

`y = x^2 - 6x - 3`

------------------------------------------------------------------

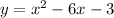
Take the coefficient of x (i.e. -6)

Divide by 2; -6/2 = -3

Square it: (-3)^2 = 9

Add and subtract the result to the equation

------------------------------------------------------------------

`y = x^2 - 6x - 3`

`y = x^2 - 6x + 9 - 9 - 3`

`y = x^2 - 6x + 9 - 12`

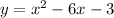
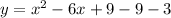
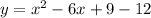
Factorize
`x^2 - 6x + 9`

`y = x^2 - 3x-3x + 9 - 12`

`y = x(x - 3)-3(x - 3) - 12`

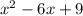
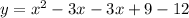
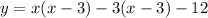
Factor out x - 3

`y = (x - 3)(x - 3) - 12`

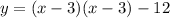
Express as squares

`y = (x - 3)^2 - 12`

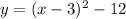
Hence, the vertex form of
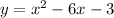`y = x^2 - 6x - 3` is:
`y = (x - 3)^2 - 12`

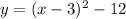
Solving (b): State the coordinates of the vertex.

In
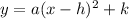`y = a(x - h)^2 + k`; the vertex is: (h,k)

The vertex of
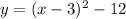`y = (x - 3)^2 - 12` will be
`(3,-12)`