Question

Segment DE has endpoints at D(2, - 8) and E(-4, 4) . If it is dilated about the origin by a factor of 4, which of the following would be the length of its image, D’E’

1.) 6sqrt(5);

2.) 24sqrt(5);

3.) 144sqrt(5);

4.) 10sqrt(5);

Answer 1

answer 2) 24
`√(5)`

Explanation:

after the dilation pt D is (8,-32)

after the dilation pt E is (-16,16)

if you use the distance formula for these two points you get
`√(2880)` which simplifies to 24
`√(5)`

Answer 2

The length of D'E' is ) 24√(5).

To solve this, we can follow these steps:

Find the original length of DE:

Use the distance formula:
`((x2 - x1)^2 + (y2 - y1)^2)`

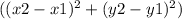
Substitute D(2, -8) and E(-4, 4): sqrt((-4 - 2)² + (4 - (-8))²) = √(36 + 144) = √(180) = 6√(5)

Apply the dilation factor:

The dilation factor multiplies the original length by the factor.

Therefore, the length of D'E' = 4 * 6√(5) = 24√(5)

Therefore, the correct answer is 2) 24√(5).