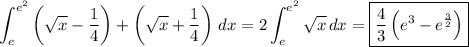Question

`\tiny\int_(e)^{{e}^(2)} \left( \sqrt{x + (1)/(2) \sqrt{x + (1)/(4) \sqrt{x + (1)/(8) \sqrt{x + (1)/(16) \dots} } } } \: + \sqrt{x - (1)/(2) \sqrt{x - (1)/(4) \sqrt{x - (1)/(8) \sqrt{x - (1)/(16) \dots} } } } \right) dx \\`

Answer 1

We have the identity

`\left(\sqrt x + \frac1{2^n}\right)^2 = x + \frac1{2^(n-1)} \sqrt x + \frac1{2^(2n)}`

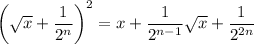
Take the square root of both sides and rearrange terms on the right to get

`\sqrt x + \frac1{2^n} = \sqrt{x + \frac1{2^(n-1)} \left(√(x) + \frac1{2^(n+1)}\right)}`

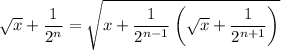
Decrementing n gives

`\sqrt x + \frac1{2^(n-1)} = \sqrt{x + \frac1{2^(n-2)} \left(√(x) + \frac1{2^(n)}\right)}`

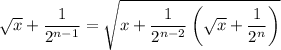
and substituting the previous expression into this, we have

`\sqrt x + \frac1{2^(n-1)} = \sqrt{x + \frac1{2^(n-2)} \sqrt{x + \frac1{2^(n-1)} \left(\sqrt x + \frac1{2^(n+1)}\right) } }`

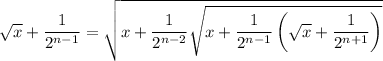
Continuing in this fashion, after k steps we would have

`\sqrt x + \frac1{2^(n-k)} = \sqrt{x + \frac1{2^(n-(k+1))} \sqrt{x + \frac1{2^(n-k)} \sqrt{x + \frac1{2^(n-(k-1))} \sqrt{\cdots \frac1{2^(n-1)} \left(\sqrt x + \frac1{2^(n+1)}\right)}}}}`

After a total of n - 2 steps, we arrive at

`\sqrt x + \frac14 = \sqrt{x + \frac12 \sqrt{x + \frac1{2^2} \sqrt{x + \frac1{2^3} \sqrt{\cdots \frac1{2^(n-1)} \left(\sqrt x + \frac1{2^(n+1)}\right)}}}}`

Then as n goes to infinity, the first nested radical converges to √x + 1/4. Similar reasoning can be used to show the other nested radical converges to √x - 1/4. Then the integral reduces to

`\displaystyle \int_e^(e^2) \left(\sqrt x - \frac14\right) + \left(\sqrt x + \frac14\right) \, dx = 2 \int_e^(e^2) \sqrt x \, dx = \boxed{\frac43 \left(e^3 - e^(\frac32)\right)}`