Which of the following shows that the sum of two irrational numbers can be irrational? A. (5+π)+(3-π) B. √3+√5 C. (3+√5)+(3-√5) D. (π/3)+(-π/3) help?

Question

asked Nov 2, 2022 61.2k views

1 Answer

Andrey Vaganov · Answer 1 · 2022-11-08T22:31:43+0000

Given:

The sum of irrational number in the options.

To find:

The option that shows the sum of two irrational numbers can be irrational.

Solution:

In option A,

$(5+\pi)+(3-\pi)=5+\pi+3-\pi$

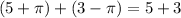
$(5+\pi)+(3-\pi)=5+3$

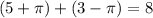
$(5+\pi)+(3-\pi)=8$

We know that 8 is a rational number. So, option A is incorrect.

In option B,

√(3)+√(5)

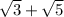
Here both numbers are irrational and it cannot be simplified further.

So,
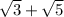√(3)+√(5) is an irrational number and option B is correct.

In option C,

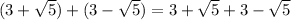
(3+√(5))+(3-√(5))=3+√(5)+3-√(5)

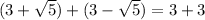
(3+√(5))+(3-√(5))=3+3

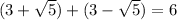
(3+√(5))+(3-√(5))=6

We know that 6 is a rational number. So, option C is incorrect.

In option D,

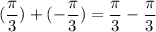
$((\pi)/(3))+(-(\pi)/(3))=(\pi)/(3)-(\pi)/(3)$

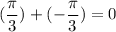
$((\pi)/(3))+(-(\pi)/(3))=0$

We know that 0 is a rational number. So, option D is incorrect.

Therefore, the correct option is B.