Question

Which of the following shows that the sum of two irrational numbers can be irrational?

A. (5+π)+(3-π)

B. √3+√5

C. (3+√5)+(3-√5)

D. (π/3)+(-π/3)

help?

Answer 1

Given:

The sum of irrational number in the options.

To find:

The option that shows the sum of two irrational numbers can be irrational.

Solution:

In option A,

`(5+\pi)+(3-\pi)=5+\pi+3-\pi`

`(5+\pi)+(3-\pi)=5+3`

`(5+\pi)+(3-\pi)=8`

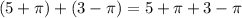
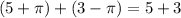
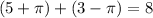
We know that 8 is a rational number. So, option A is incorrect.

In option B,

`√(3)+√(5)`

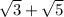
Here both numbers are irrational and it cannot be simplified further.

So,
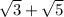`√(3)+√(5)` is an irrational number and option B is correct.

In option C,

`(3+√(5))+(3-√(5))=3+√(5)+3-√(5)`

`(3+√(5))+(3-√(5))=3+3`

`(3+√(5))+(3-√(5))=6`

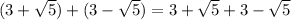
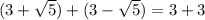
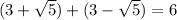
We know that 6 is a rational number. So, option C is incorrect.

In option D,

`((\pi)/(3))+(-(\pi)/(3))=(\pi)/(3)-(\pi)/(3)`

`((\pi)/(3))+(-(\pi)/(3))=0`

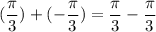
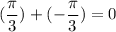
We know that 0 is a rational number. So, option D is incorrect.

Therefore, the correct option is B.