Question

Derive the expression for electrical-loading nonlinearity error (percentage) in a rotatory potentiometer in terms of the angular displacement, maximum displacement (stroke), potentiometer element resistance, and load resistance. Plot the percentage error as a function of the fractional displacement for the three cases: RL/RC = 0.1, 1.0, and 10.0

Answer 1

The plot for percentage error as a function of fractional displacement (
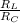`(R_(L) )/(R_(C) )`) for the values of 0.1,1.0,10.0 is shown in image attached below.

Step-by-step explanation:

Electrical loading non linearity error (percentage) is shown below.

`E=(((v_(o) )/(v_(r) )-(Q)/(Q_(max) ) ))/((Q)/(Q_(max) ) )`×
`100`

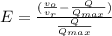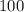
where Q= displacement of the slider arm

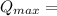`Q_(max)=` maximum displacement of a stroke

`(v_(o) )/( v_(r) ) =`
`(((Q)/(Q_(max) )((R_(L) )/(R_(C) ) ) ))/(((R_(L) )/(R_(C) ) ) +((Q)/(Q_(max) ))-((Q)/(Q_(max) ))^(2) )`

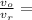
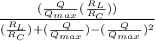
here
`R_(L)=load resistance`

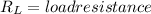
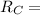`R_(C)=`total resistance of potentiometer.

Now the nonlinearity error in percentage is

`E=(((((Q)/(Q_(max) )((R_(L) )/(R_(C) ) ) ))/(((R_(L) )/(R_(C) ) ) +((Q)/(Q_(max) ))-((Q)/(Q_(max) ))^(2) )-(Q)/(Q_(max) ) ))/((Q)/(Q_(max) ) )`×
`100`

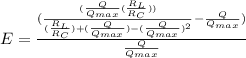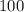
The following attached file shows nonlinear error in percentage as a function of
`(R_(L) )/(R_(C) )` displacement with given values 0.1, 1.0, 10.0. The plot is drawn using MATLAB.

The MATLAB code is given below.

clear all ;

clc ;

ratio=0.1 ;

i=0 ;

for zratio=0:0.01:1 ;

i=i+1 ;

tratioa (1,i)=zratio ;

E1(1,i)=((((zratio*ratio)/(ratio+zratio-zratio^2))-zratio)/zrtio)*100 ;

end

ratio=1.0 :

i=0 ;

for zratio=0:0.01:1 ;

i=i+1 ;

tratiob (1,i)=zratio ;

E2(1,i)=((((zratio*ratio)/(ratio+zratio-zratio^2))-zratio)/zratio)*100 ;

end

ratio=10.0 :

i=0 ;

for zratio=0:0.01:1 ;

i=i+1 ;

tratioc (1,i)=zratio ;

E3(1,i)=((((zratio*ratio)/(ratio+zratio-zratio^2))-zratio)/zrtio)*100 ;

end

k=plot(tratioa,E1,tratiob,E2,tratioc,E3)

grid

title({non linear error in % as a function of R_L/R_C})

k(1). line width = 2;

k(1).marker='*'

k(1).color='red'

k(2).linewidth=1;

k(2).marker='d';

k(2).color='m';

k(3).linewidth=0.5;

k(3).marker='h';

k(3).color='b'

legend ('location', 'south east')

legend('R_L/R_C=0.1','R_L/R_C=1.0','R_L/R_C=10.0')