Answer:
V = 27948.09 cubic feet
Explanation:
Given that,
A farmer's silo is in the shape of a cylinder topped by a hemisphere.
The radius of silo, r = 13 ft
Height of the cylindrical portion, h = 44 ft
We need to find the volume of the silo. Net volume is equal to :
V = Volume of cylinder + volume of hemisphere
i.e.
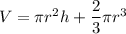
Put all the values,
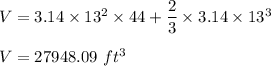
Hence, the volume of the silo is equal to 27948.09 cubic feet.