Question

Consider the equation:

6x+55=x^2
1) Rewrite the equation by completing the square.
Your equation should look like (x+c)^2=d(x+c)
2
=dleft parenthesis, x, plus, c, right parenthesis, squared, equals, d or (x-c)^2=d(x−c)
2
=dleft parenthesis, x, minus, c, right parenthesis, squared, equals, d.
2) What are the solutions to the equation?

Answer 1

Explanation:

1.

Subtract the coefficient from both sides, keep 55 on the same side.

`{x}^(2) - 6x = 55`

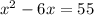
Complete the square by dividing the coefficient by two and squaring it.

`{x}^(2) - 6x + 9 = 55 + 9`

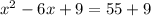
Use binomial to factor the left side.

`(x - 3) {}^(2) = 64`

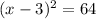
2. Solve for x.

`(x - 3) = 8`

`x = 11`

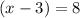
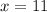
Remeber the square root of 64 is also -8 so

`x - 3 = - 8`

`x = - 5`

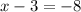
So the solutions are -5 and 11

Answer 2

Answers

1) We can rewrite the equation as 64=(x−3)^2

2) The solutions to the equation are x=3±8