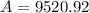Answer:
$9520.92
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
Compounded Interest Rate Formula:
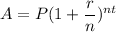
- P is principle amount
- r is rate
- n is compounded rate
- t is time
Explanation:
Step 1: Define
Identify variables
P = 5500
r = 5.5% = 0.055
n = 12
t = 10
Step 2: Find A
- Substitute in variables [Compounded Interest Rate Formula]:
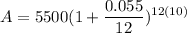
- (Parenthesis) Divide:
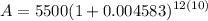
- (Parenthesis) Add:
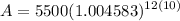
- [Exponents] Multiply:
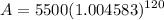
- Evaluate exponents:
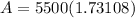
- Multiply: