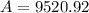Question

You deposit $5,500 into a saving account that pays an annual interest rate of 5.5% compounded monthly.

How much would you have after 10 years?

Answer 1

$9520.92

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Compounded Interest Rate Formula:
`\displaystyle A = P(1 + (r)/(n))^(nt)`

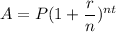
• P is principle amount
• r is rate
• n is compounded rate
• t is time

Explanation:

Step 1: Define

Identify variables

P = 5500

r = 5.5% = 0.055

n = 12

t = 10

Step 2: Find A

1. Substitute in variables [Compounded Interest Rate Formula]:
   `\displaystyle A = 5500(1 + (0.055)/(12))^(12(10))`
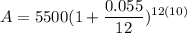
2. (Parenthesis) Divide:
   `\displaystyle A = 5500(1 + 0.004583)^(12(10))`
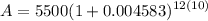
3. (Parenthesis) Add:
   `\displaystyle A = 5500(1.004583)^(12(10))`
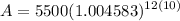
4. [Exponents] Multiply:
   `\displaystyle A = 5500(1.004583)^(120)`
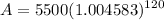
5. Evaluate exponents:
   `\displaystyle A = 5500(1.73108)`
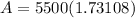
6. Multiply:
   `\displaystyle A = 9520.92`