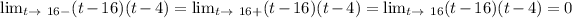Question

Let ​g(t)= t−16 t−4. a. Make two​ tables, one showing the values of g for t=15​.9, 15​.99, and 15.999 and one showing values of g for t=16​.1, 16​.01, and 16.001. b. Make a conjecture about the value of limt→16 t−16 t−4.

Answer 1

`\lim_(t \to \ 16) (t-16)(t-4) =0`

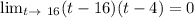
Explanation:

g(t)= (t-16)(t-4)

(a) Then, we have,

t g(t)

15.9 -1.19

15.99 -0.1199

15.999 -0.011999

Also, we have,

t g(t)

16.1 1.21

16.01 0.1201

16.001 0.012001

(b) We can see, from the above table that as 't' tends to 16 from the left hand side, the value of g(t)= (t-16)(t-4) is tending to 0 from the negative direction.

Similarly, from the second table, we can see that as 't' tends to 16 from the right hand side, the value of g(t)= (t-16)(t-4) is tending to 0 from the positive direction.

Thus, we can say that
`\lim_(t \to \ 16-) (t-16)(t-4)` &
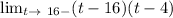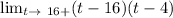`\lim_(t \to \ 16+) (t-16)(t-4)`, i.e., the left hand limit and right hand limit of g(t)= (t-16)(t-4), at t=16, both exist and is both equal to 0.

Since both these limits exist and are equal, we can say,
`\lim_(t \to \ 16-) (t-16)(t-4) = \lim_(t \to \ 16+) (t-16)(t-4) = \lim_(t \to \ 16) (t-16)(t-4) = 0`